Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.
Advertisement
Scientific Reports volume 14, Article number: 30971 (2024)
Metrics details
In order to investigate the influence of shear on contact characteristics and fluid flow evolution of rough rock fractures, a series of shear-flow tests were carried out by numerical experiments. Firstly, a sandstone specimen with a rough fracture was made in the laboratory, and the numerical model of the fracture was reconstructed in FLAC3D software. Experiments were conducted to investigate the depth of penetration of the fracture under different normal stress (1, 3, and 5 MPa) and shear displacement (2, 4, 6, 8, and 10 mm). By establishing the relationship between the shear direction and the apparent inclination of the fracture asperity, the effects on the asperity contact characteristics and seepage properties are explored. The results of the study indicated that the larger the normal stress the larger the surface contact section and the smaller the aperture, showing the opposite trend with increasing shear displacement. Positive apparent inclination distribution can effectively predict the location of shear damage during the shear process. Negative apparent dip implies that those regions increase permeability after shear, and decrease with increasing crack opening. Fracture seepage shows obvious nonlinear characteristics, where the nonlinear coefficients are 5–6 orders of magnitude larger than the linear coefficients. The critical Reynolds number Rec is used to distinguish the linear and nonlinear categories of fluid flow, and the calculated results show that the range of Rec is between 0.0081 and 0.11.3, and the Rec increases with shear displacement and decreases with normal stress.
There are a large number of fracture joints within the rock mass, and numerous engineering practices have demonstrated that the stability of projects is closely related to the slip failure of these discontinuous surfaces1,2,3,4,5. For instance, disturbances generated during underground mining activities and tunneling can activate faults, leading to failures that pose significant risks to mining spaces. Earthquakes and rockbursts, which result from mining-induced fault slips, are among the primary hazards impacting underground safety6,7. Consequently, an in-depth study of the shear properties of fractures holds great significance for guiding engineering practices in the prevention and control of engineering disasters.
The distance between the upper and lower surfaces of a fracture, known as the aperture, serves as the primary channel for fluid flow. Numerous fissure joints are distributed throughout natural rock masses, and understanding fluid flow in a single fissure is fundamental to modeling seepage in complex fracture networks8. Typically, fracture flow can be described by the Navier-Stokes Equation9. However, due to the complexity of solving the NS equation, the inertia term is often neglected, leading to a simplified form10,11,12. The cubic law, which expresses the flow rate and permeability coefficient of a fissure as a linear relationship, is derived by assuming the upper and lower surfaces of the fracture act as parallel plates. Yet, in nature, joint surfaces are rough, and the complexity of surface morphology along with high water pressure can cause seepage to deviate from the linear cubic law. In such cases, the cubic law overestimates the transmissivity of the fracture13,14. Scholars often characterize this nonlinearity using the Forchheimer formula, which includes both primary and secondary flow forms and has been verified for its accuracy in describing nonlinear seepage15,16,17. Ronget et al. noted that this equation does not account for the effect of crack surface geometry on seepage, thus failing to explain the triggering mechanism of nonlinear seepage due to fracture surface contact and roughness18. Chen et al. indicated that the roughness, contact area, and tortuosity of the cracks generate inertial forces, leading to nonlinear seepage19. Similar conclusions were reached by Bursh and Thomson in their study, concluding that complex flow lines in a laminar state also result in inertia losses20. Gao et al. proposed a new theoretical model for predicting the nonlinear flow behavior in rough rock fractures under shear, effectively characterizing the nonlinearity of fluid flow by combining the Darcy-Weisbach equation with the Izbash equation21.
Many factors affecting nonlinear flow in fractures, such as roughness, normal stress, and fracture aperture, were investigated in previous studies. These studies usually select a critical value to define whether the fluid is in a linear flow state or not, such as the critical flow rate, the critical hydraulic gradient, or the critical Reynolds number. Ranijth and Darlington studied the effect of normal pressure on seepage and found that Rec decreases with increasing normal stress22. Wang et al. noted that the JRC and Rec values of the fracture exhibit a negative exponential relationship23. Liu et al. found that an order of magnitude up in fracture aperture decreases the critical hydraulic gradient by a multiple of about 1,00024.
The above studies mainly focused on conformable contact fractures. However, joint fractures are weak segments in the rock mass and are prone to shear failure along discontinuous surfaces. The evolution of contact relations and aperture distribution of fracture walls induced by shear displacement is the main factor affecting the fluid flow state in rough fractures25,26,27. Rong (2016) investigated the shear-fluid behavior of roughness cracks with different JRC and showed that the shear displacement increased from 0 to 10 mm, corresponding to critical Reynolds number values from 1.5 to 1324. Yin et al. indicated that critical hydraulic gradient is positively correlated with shear displacement and negatively correlated with normal stress27. Through the review of the above studies, most of the studies focused on the effect of JRC and positive stress on nonlinear seepage in shear. It has been pointed out that the contact area of the fracture is also an important factor affecting the phenomenon. However, laboratory tests or empirical equations are difficult to quantitatively describe the laws of fracture contact area and aperture evolution during shear, and numerical simulation provides an excellent alternative.
Although previous studies have extensively investigated the fluid flow characteristics in rough fractures, there has been a lack of in-depth understanding and quantitative description of the dynamic evolution of fracture contact characteristics and aperture distribution during shear, as well as how these factors influence the nonlinear characteristics of fluid flow. Building on this foundation, we developed a numerical simulation framework for fluid flow in shear-induced rough fractures to delve into the evolution of fracture contact characteristics and aperture distribution. Using the INTERFACE module in FLAC3D, we conducted a detailed study of the dynamic contact behavior of fractures during shear, while the application of COMSOL software has enabled us to analyze the fluid flow characteristics of sheared fractures. In this study, we also considered the relationship between the shear direction and the micro-slope of the fracture, analyzing the significant role of the apparent dip angle in predicting the damage areas and flow line distribution in rough shear fractures. Furthermore, we systematically analyzed the sensitivity of key parameters such as fracture contact area, aperture frequency, nonlinear fluid flow parameters, normalized permeability, and critical Reynolds number under different normal stress and shear displacement conditions.
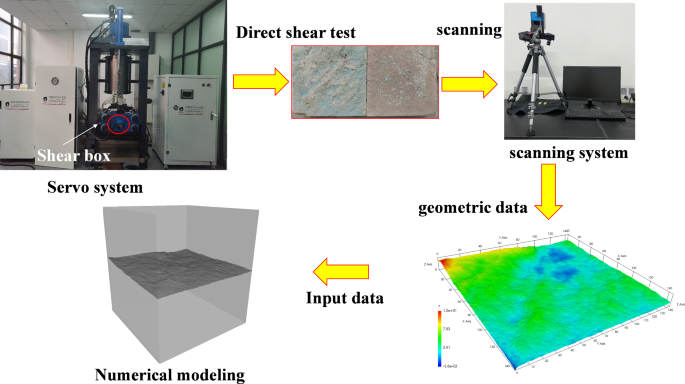
Initially, a cubic sandstone specimen measuring 150 × 150 × 150 mm was prepared. An initial fracture was introduced through a split test conducted on the specimen. The direct shear test was then carried out using the RMT301 shear testing system, which is capable of withstanding a maximum horizontal load of 500 kN and a maximum vertical load of 1500 kN. The shear test was performed under a constant normal stress boundary condition. After the normal load was applied at a rate of 0.5 kN/s, reaching 3 MPa, the bottom shear box was loaded at 0.5 kN/s to provide the shear load. The loading was ceased once the shear displacement reached 10 mm.
Experimental equipment and joint modeling.
The three-dimensional scanning equipment used in this study is the JR-AF model 3D scanner provided by Beijing JiRuiXinTian Technology Co., Ltd., featuring non-contact grating photogrammetry scanning technology with high precision measurement capabilities, achieving a scanning accuracy of ± 0.015 mm, providing accurate 3D data for the experiment. The roughness of the fracture was quantified using the Joint Roughness Coefficient (JRC), which was calculated with reference to the established methods28:
where Zi represents the crack opening, n is the number of data points, and (Delta x)is the spacing between data points. In our tests, n is 2061 and the spacing is 0.0028, and JRC is calculated as 5.75. The high-precision non-contact 3D laser scanner was employed to capture the fracture morphology data (see Fig. 1). Subsequently, the scanned data were imported into FLAC3D to construct the numerical fracture model.
In this study, the INTERFACE module within FLAC3D was utilized to investigate the dynamic contact behavior of rock fracture surfaces under compressive shear. The developed model comprised 50,000 zone elements, 9,236 element nodes, 2,601 INTERFACE nodes, and 5,000 INTERFACE elements (Fig. 1). The shear properties of rock fractures are influenced by the shear direction, which is primarily manifested through the interaction between the inclination of micro-bumps and the direction of shear29. FLAC3D divides the INTERFACE elements into two triangular elements. The apparent inclination is defined as the angle between a line within a triangular element along the shear direction and its horizontal projection30. This apparent inclination can be determined using the coordinates of the INTERFACE nodes and the shear direction vector:
The micro-slope angle of the asperities varies from 0° to 90° as the upper and lower surfaces interact. As they move in opposite directions, the magnitude of the asperity micro-slope angle ranges from 0° to -90°, at which point the fractures may open, creating highly permeable channels (as illustrated in Fig. 2).
Characterization of fracture surface structure.
The penetration depth of INTERFACE can indicate the contact state of the fracture. When the penetration depth is greater than zero, the element node penetrates the surface of the element and overlaps the element (see Fig. 3). It has been shown that these overlaps can be a reasonable representation of the contact area in a shear test31.
Depth of penetration and contact relationships.
For this numerical test, three sets of shear test programs were designed. The normal stresses are set to 1, 3, and 5 MPa. Applying load to the Matrix below the fracture at a rate of 1 × 10− 6 m/step. The constraints is described in Fig. 3. The penetration depth (delta n) and contact area of INTERFACE at shear displacements (Delta u)= 2, 4, 6, 8, and 10 mm, were recorded for each set of test. The fracture aperture in regions with penetration depths > 0 is zero, and in regions with penetration depths < 0 are their opposites (see Eq. 4). In this way, a three-dimensional aperture model is established. The seepage tests for different fracture patterns were carried out in COMSOL software.
FLAC3D software provides the INTERFACE module to address issues of sliding or separation in geomechanics. The Coulomb sliding criterion is employed to describe the shear stresses during interface sliding. If the normal stress is tensile, the element cannot undergo shear stress. The FLAC3D program calculates the absolute penetration velocity and relative shear velocity for each time step, which are used to determine the normal and shear stresses. The intrinsic model of the fracture surface is defined by a linear Coulomb shear strength criterion. This criterion limits the tangential and normal forces at the interface nodes, the normal and shear stiffness, the shear bond and tensile strengths, and the shear dilation angle. The normal and shear forces that describe the elastic interface response are determined in real-time using the following relations:
The Coulomb shear-strength criterion restricts the shear force by the relation:
where c represents the cohesion along INTERFACE; (varphi) is the friction angle of the surface of the structural face. The INTERFACE element has two states, bonded and broken. Once the element yielded either by reaching shear strength (Eq. 7) or tensile strength, it no longer bears tensile stress.
In this study, the dilation angle of the shear plane is assumed to be zero. This assumption is based on the premise that the normal lift due to shear slip is primarily dictated by the intrinsic morphology of the structural surface. Consequently, the dilation angle is set to zero to align with this premise. The specific physical parameters that underpin our model are presented in Table 1.
In the context of fracture seepage processes, water is characterized as a viscous, incompressible fluid, and its behavior is commonly modeled using the Navier-Stokes (NS) Equations20,32,33. These equations encapsulate the dynamics of fluid flow by incorporating inertial forces, pressure gradients, viscous forces, and any external forces that may influence the fluid’s motion.
where ρ is the density; P is the fluid pressure; f is the volumetric force acting on the fluid; T is the shear stress of the fluid; (nabla) is the Hamiltonian operator; u is the fluid flow rate.
The expression of the continuity equation for an incompressible fluid is given by:
Cube’s law is used to calculate the relationship between flow and pressure gradient for smooth parallel fractures, where the permeability of the fracture is controlled by the aperture of the fracture.
where w is the fracture width; e is the fracture aperture; Q is the volume flow rate.
When the water velocity exceeds a certain threshold, the flow rate and pressure gradient are not in a linear relationship34. The nonlinear seepage formula is expressed by a quadratic binomial equation, where the first term represents linear seepage and the second term represents nonlinear seepage.
where (hat {a}= – mu /kA) is a linear coefficient; (hat {b}= – beta mu /{A^2}) is a nonlinear coefficient.
Another expression of the Forchheimer formula can be obtained from the relationship between hydraulic gradient and pressure:
where (J=frac{P}{{rho g}})is hydraulic gradient; (a=frac{{hat {a}}}{{rho g}}); (b=frac{{hat {b}}}{{rho g}}).
These two coefficients are related to the aperture size and the morphology of the fracture surface. Zeng and Grigg proposed a characterization method to determine the fluid flow state inside the fracture based on a large number of experiments35. E is the scale factor which is a dimensionless number between 0 and 1. E = 0.1 indicates the critical point for linear and nonlinear seepage in the fractured rock mass.
Reynolds number reflects the ratio relationship between the inertia force and the cohesion force of a fluid, and can be used to characterize the nonlinear characteristics of a fluid.
where Re is the Reynolds number; µ is the fluid viscosity.
Figure 4(a) illustrates the apparent inclination of the shear direction within the numerical model, where varying colors denote distinct angles of inclination. Figure 4(b) captures the characteristics of shear damage on the fracture’s rough surface as observed in the laboratory setting. In Fig. 4(b), the blue areas specifically highlight regions that have experienced shear damage. Conversely, in Fig. 4(a), regions depicted in hues closer to red signify a steeper apparent dip angle, suggesting that these areas are prone to exhibit relative extrusion of the fracture’s asperities during shear deformation. It is evident that there is a significant correlation between the regions of shear damage identified in Fig. 4(b) and those with a higher apparent dip angle in Fig. 4(a). Furthermore, areas with an apparent inclination angle below zero, indicating a reverse slope, result in a separation of the fracture’s upper and lower surfaces post-shear testing. In the case of the rough fracture under examination, the negative apparent dip angles, primarily located in the lower left quadrant of Fig. 4(a), are anticipated to correspond to zones of enhanced permeability following shear. This permeability will be further explored in the subsequent seepage test outcomes. Overall, the numerical simulation methodology outlined in this paper effectively replicates the contact characteristics throughout the shear process of the fracture.
Distribution of (a) the angle of visual inclination, (b) shear damage in laboratory tests.
Figure 5 illustrates the relationship between shear stress and displacement, including a comparison between experimental and simulation results. During the initial stage of shear displacement (0–7.5 mm), shear stress increases nonlinearly with the increase in displacement, indicating the mechanical behavior of the material as it transitions from elastic to plastic deformation. The peak shear stress is reached at approximately 7.5 mm of displacement, signifying the maximum shear strength of the material. The occurrence of peak stress suggests that the material experiences the most significant shear resistance at this displacement.
Following the peak, the shear stress begins to decline, a trend that may be associated with the propagation of micro-cracks within the material or a reduction in frictional effects. As displacement continues to increase, the shear stress stabilizes after 10 mm, which could imply that the material has reached a new state of equilibrium or that damage has become stable.
The simulation results correspond well with the experimental data across most of the range, particularly before the peak shear stress is attained. This validation confirms the effectiveness of the simulation method in predicting the shear behavior of the material. However, there is a noticeable discrepancy between the simulation and experimental results after the peak stress, which may be due to the simulation not fully capturing the complexity of the material’s behavior.
Shear test displacement-stress curve.
The aperture of a fracture is a pivotal factor influencing seepage flow, with this aperture being characterized by the penetration depth. As delineated in Sect. 2.1, fractures are categorized into regions of contact and non-contact based on specific criteria (Fig. 6(a)). In these regions, a negative penetration depth signifies the presence of a seepage channel, where the aperture’s magnitude is equivalent to the absolute value of the penetration depth, as depicted in Fig. 6(a). The green areas indicate zones of contact where the fracture aperture is effectively closed during the fluid flow experiments. Figure 6(b) presents the calculated distribution of penetration depths for the INTERFACE elements under a normal stress of 3 MPa and a shear displacement of 2 mm. The distribution aligns with a normal distribution pattern, with a maximum aperture of 0.719 mm. Concurrently, the laboratory-measured maximum normal displacement of 0.683 mm substantiates the accuracy of the numerical simulation.
Distribution of (a) the angle of visual inclination, (b) shear damage in laboratory tests.
Figure 7 illustrates the distribution of penetration depths for the INTERFACE elements throughout the shearing process. The colored regions denote areas of contact depth, while the white regions indicate areas of separation. It is evident that as the shear displacement increases, the contact area diminishes, and the penetration depth augments, a phenomenon attributable to stress concentration. To elucidate, consider the contact area’s evolution under a constant normal stress of 3 MPa. At shear displacements of 0, 2, 4, 6, 8, and 10 mm, the contact area’s proportion relative to the total interface area is 100%, 67.53%, 42.76%, 32.77%, 31.52%, and 24.45%, respectively. Correspondingly, the maximum contact depths recorded are 0, 0.58, 0.94, 1.19, 1.52, and 1.69 mm.
Contour plot of penetration depth distribution on fracture surface under (a) 1 MPa, (b) 3 MPa, and (c) 5 MPa normal load.
Figure 8 depicts the correlation between shear displacement and the proportion of contact area under varying normal stress conditions. As the normal stress increases, the rate of reduction in the contact area diminishes. This trend is attributed to the increased resistance to separation within the fracture under higher normal stress, which suppresses dilatancy. Consequently, the contact depth increases, and the aperture of the fracture decreases. Specifically, at normal stresses of 1, 3, and 5 MPa, the maximum contact depths recorded are 1.35 mm, 1.69 mm, and 1.94 mm, respectively.
Contact area versus shear displacement under 1, 3, and 5 MPa normal loads.
Figure 9 presents the frequency distribution characteristic curves of INTERFACE penetration depths at a constant normal stress of 3 MPa across various shear displacements. The curves exhibit several notable characteristics:
The peak frequencies for different shear displacements are consistently located within the range of penetration depths, suggesting that the mean (µ) of the frequency distribution remains relatively stable.
As the shear displacement increases, the peak value of the frequency curve diminishes, while the curve’s spread widens. This indicates an increase in the maximum aperture of the fracture.
Throughout the testing, the area designated as the separation zone, where the penetration depth is negative, expands progressively with greater shear displacement. The contact area experiences a significant reduction when the shear displacement is below 4 mm, with minimal further change observed beyond 6 mm.
Specifically, at shear displacements of 2, 4, 6, 8, and 10 mm, the mean penetration depths are 0.086 mm, -0.058 mm, -0.21 mm, -0.24 mm, and − 0.42 mm, respectively. Correspondingly, the standard deviations are 0.186 mm, 0.38 mm, 0.52 mm, 0.60 mm, and 0.73 mm.
Penetration distributions of fractures under different shear displacement.
Figure 10 illustrates the frequency distribution characteristic curve of INTERFACE penetration depths at a shear displacement of 6 mm. As the normal stress increases, there is a corresponding increase in both the contact area and the maximum penetration depth of the structural plane. While normal stress exerts minimal influence on the overall shape of the frequency curve, it does affect the curve’s position. Specifically, an increase in normal stress shifts the curve to the right, reducing the mean value of penetration depth, while the standard deviation remains relatively unaffected. The relationship between normal stress and contact depth is linear, a finding consistent with the research of Wang et al.36. This linearity is attributed to the geometry of the fracture surface and the direction of shear during the shearing process. The enhancement of normal stress leads to an increased penetration depth at the convexities of the fracture surface, thereby expanding the contact area.
Penetration distributions of fractures under different normal load.
Figure 11 presents the characteristic distribution of fluid streamlines within the fracture under varying conditions of normal stress and shear displacement at a constant hydraulic gradient (J = 1). The flow is oriented perpendicularly to the direction of shear, resulting in a pronounced grooving effect. This effect arises from the morphological alterations and the separation occurring at the fracture’s rough surfaces. As observed in Fig. 6, the white regions, indicative of separation areas, correspond to the primary distribution of streamlines. It is evident that an increase in normal stress leads to a reduction in the number of streamlines, with a concurrent increase in their density within the dominant flow channel. This suggests that higher normal stresses constrict fluid movement, localizing it within the primary channel. The compressive effect of elevated normal stress confines the fluid, thereby compacting the streamlines within this channel.
Moreover, as shear displacement augments, there is an initial increase in the number of streamlines, with the distribution becoming relatively stable once the displacement surpasses 2 mm. Notably, the predominant region of negative apparent inclination angles aligns with the lower section of the flow outlet depicted in Fig. 10. Prior analyses have indicated that these regions with negative apparent inclination angles are associated with enhanced fracture permeability post-shearing. The streamlines in Fig. 11 exhibit a propensity to diverge downward from the intended hydraulic slope direction, which is horizontal to the right. This divergence demonstrates that the distribution of apparent inclination angles significantly influences the seepage behavior of the fracture following shear. The impact of these angles is contingent upon the normal stress and shear displacement conditions to which the fracture is subjected.
In general, the influence of local variations in permeability, attributed to the stochastic distribution of fracture asperities, diminishes as the fracture aperture widens. This is because the larger aperture tends to average out the effects of localized asperity distribution on the overall flow pattern.
Flow streamlines for different shear displacements under (a) 1 MPa; (b) 3 MPa; and (c) 5 MPa normal load.
Figure 12 depicts the relationship between the hydraulic slope (J) and the volumetric flow rate (Q). This figure documents the behavior of fracture flow across a spectrum of normal stresses, with the hydraulic slope varying from 0.1 to 10. In accordance with Eq. 12, the curves plotting volumetric flow against hydraulic slope display distinct nonlinear traits. The collected monitoring data have been fitted using a quadratic model, yielding goodness-of-fit coefficients (R2) that exceed 0.99, indicating a high degree of model accuracy.
At lower shear displacements, the curves exhibit steeper slopes, reflecting the subtle initial growth of cracks. Conversely, under conditions of elevated normal stress, a more substantial hydraulic gradient is necessary to achieve an equivalent flow rate. It is noteworthy that in the C5-2 test, the linear coefficients of the J-Q relationship significantly surpass those of the nonlinear terms. This suggests that, under these specific conditions, the flow of water through the fracture can be approximated as linear. This observation will be subjected to further scrutiny in subsequent analyses.
Relationships between the hydraulic gradient and volumetric flow rate during the shear process.
The Forchheimer equation is extensively utilized to characterize nonlinear seepage behavior. Utilizing Eq. 10, the linear coefficient a and the nonlinear coefficient b were determined. Both coefficients exhibit a decline as shear displacement increases, with a more pronounced rate of decrease observed in the range of 2 to 4 mm compared to 4 to 10 mm. The nonlinear coefficient b is significantly larger, being 5 to 6 orders of magnitude greater than the linear coefficient a, a trend also observed in reference8. It is established that a is inversely related to the permeability coefficient; hence, as normal stress increases, reducing fracture permeability, the positive correlation between a and normal stress is evident in the distinct curves of Fig. 13.
The value of b is derived from the quadratic relationship with the cross-sectional area A of the flow. With increasing shear displacement, the contact area within the fracture diminishes, and the aperture expands. Consequently, the flow’s curvature reduces, leading to a decrease in b. Notably, the C5-2 dataset displays pronounced linear behavior, with a values substantially higher and b values considerably lower than those of other groups. This can be correlated with Fig. 7, which indicates a large fracture contact area and poor fracture connectivity, restricting fluid flow to a limited channel, as depicted in Fig. 11, thereby accentuating the linear flow characteristic.
Relationships between the forchheimer coefficient and shear displacement.
Based on Eq. (14), the relationship between shear displacement and critical flow is plotted (as shown in Fig. 14), and in general these two variables show a negative correlation law. In addition, the critical flow rate exhibits a negative correlation with normal stress, a phenomenon that can be ascribed to the influence of fracture aperture on the variation in nonlinear seepage. As demonstrated by Schrauf and Evans37, variations in flow velocity along the seepage path lead to a loss of fluid inertia, which is a primary cause of nonlinear seepage. The modification of crack openings within the seepage path induces adjustments in water velocity to adhere to the principle of mass conservation. The interplay of fluid acceleration and deceleration causes the relationship between the hydraulic gradient and the volumetric flow rate to diverge from linearity, as discussed in reference23.
The nonlinearity of flow within fractures is intricately linked to the aperture field’s distribution. Given the rugged nature of fracture morphology, shear displacement prompts the rough surfaces to slide against each other, leading to an irregular pattern of grooves and protrusions. The flow path is governed by the fracture’s aperture, as illustrated in Fig. 9, where an increase in displacement corresponds to a greater standard deviation ((:sigma:)) of aperture sizes. This signifies a broader range of aperture distributions and a more intricate seepage network. The heterogeneous pore size distribution is conducive to the manifestation of nonlinear flow characteristics.
Relationship between the critical volume flow and shear displacement.
Transmissivity is a crucial parameter for evaluating the flow characteristics of fluids within fractures. Typically, the relationship between transmissivity and the Reynolds number (Re) is employed to delineate the linear and nonlinear flow regimes. The intrinsic permeability coefficient, denoted as T0, is a constant that is independent of the flow rate and reflects the inherent capacity of the fracture channel to transmit fluid. The apparent transmissivity, T, which is assessable through Eq. 11, is instrumental in evaluating nonlinear flow rates.
where T is transmissivity.
Figure 15 shows the relationships between transmissivity and Reynolds number. T exhibits a power function relationship with the Reynolds number. The transmissivity curve demonstrates a distinct bimodal behavior; for Re < 0.1, changes in Re have a negligible impact on T, whereas for Re > 0.1, T diminishes precipitously with increasing Re. Furthermore, T augments with increasing shear displacement (Δu), and the velocity of this increase is modulated by the normal stress. Higher normal stresses result in a reduced rate of change for T and a lower ultimate permeability coefficient. The relationship between T and Re was modeled using an exponential function, and the model’s accuracy was confirmed with a mean square deviation of R2 > 0.98, as depicted in Fig. 15. This fitting equation is valuable for ascertaining the intrinsic permeability of the fracture, T0.
Relationships between transmissivity and Reynolds number.
In Zimmerman’s study, the normalized transmissivity (T/T0) is correlated with both the Reynolds number (Re) and the Forchheimer coefficient (β)10.
Figure 16 presents the normalized transmissivity (T/T0) versus Reynolds number (Re) curves for a variety of compressive stress conditions. The data depicted in this figure reveal that the permeability coefficient transitions from linear to nonlinear behavior as the Reynolds number increases. The curves are observed to ascend as the shear displacement grows, with the curve corresponding to Δu = 2 mm exhibiting a notably greater offset compared to those associated with other shear displacements. This observation is in accordance with the research conducted by Wang et al.36.
Upon equivalent transformation, a normalized transmissivity of T/T0 = 0.9 is identified as having equivalent physical significance to an efficiency coefficient (E) of 0.1. The Reynolds number at this juncture is designated as the critical Reynolds number (Rec ). The values of Rec derived from this study range from 0.0081 to 0.113, which are consistent with the findings of Javadi et al.33, Rong et al.4, and Wang et al.31, whose calculations spanned a range of 0.001 to 48.73. It is important to note that, in contrast to the laboratory tests, this study’s simulation did not factor in the presence of crushed particles within the cracks, maintained a crack expansion angle of zero, and considered average crack widths that were narrower than those observed in laboratory settings.
It is noteworthy that the curve’s position ascends with increasing tangential displacement when T/T0 < 0.9 under a normal stress of 5 MPa, excluding the case where Δu = 2. This positive correlation is observed for T/T0 < 0.6 under a normal stress of 3 MPa; however, no such correlation is evident at a normal stress of 1 MPa. A comparison between the relationships derived from experimental and numerical computational methods reveals that the Forchheimer equation introduces a degree of variability in predicting experimental outcomes within the transition zone from linear to nonlinear flow, approximately in the range 5 < Re < 2010. Although this study only examines a single case, the findings from Fig. 13 clearly indicate the presence of a discernible transition zone. The magnitude of this transition zone is contingent upon the normal stress applied to the fracture; higher normal stresses result in a more confined transition area.
Relationships between normalized transmissivity and Reynolds number.
In this study, a numerical model of the same scale was constructed using FLAC3D software, with a laboratory-created fracture serving as the template. The dynamic contact characteristics during the shear process were simulated using the INTERFACE module, while the nonlinear seepage characteristics of the open space generated by shear were modeled with COMSOL software. The findings indicate the following:
As the shear displacement (Δu) increases, the contact area of the structural surface diminishes progressively, the contact depth intensifies, and the crack aperture widens. Conversely, an increase in normal stress leads to an expansion of the contact area and a reduction in the crack opening.
The distribution map of apparent inclination, which is correlated with the shear direction and the micro-slope of the fracture asperities, provides an accurate prediction of the shear damage extent within the fracture. A negative apparent inclination effectively demarcates regions of heightened permeability post-shear, influencing the pattern of flow lines. However, this influence diminishes as the crack opening enlarges.
The flow rate and the drop in hydraulic slope display a nonlinear relationship, with the Forchheimer equation adeptly characterizing the curve’s attributes. The linear coefficient and the nonlinear coefficient vary by five to six orders of magnitude. Both coefficients exhibit a negative correlation with shear displacement and a positive correlation with normal stress. The critical flow rate escalates with shear displacement and wanes with increasing normal stress.
When the transmissivity surpasses the critical Reynolds number, it transitions from linear to nonlinear behavior. The critical transmissivity (Rec) ascends with greater shear displacement and descends with higher normal stress.
Data will be made available on reasonable request to author Yu Zhao (zytyut1@126.com).
Chen, L. L., Wang, Z. F. & Wang, Y. Q. Failure analysis and treatments of tunnel entrance collapse due to sustained rainfall: A case study. Water 14, 2486. https://doi.org/10.3390/w14162486 (2022).
Article CAS MATH Google Scholar
Ma, T., Wang, L., Suorineni, F. T. & Tang, C. Numerical analysis on failure modes and mechanisms of mine pillars under shear loading. Shock Vib. 2016, 1–14. https://doi.org/10.1155/2016/6195482 (2016).
Article MATH Google Scholar
Yun, C. et al. Micro-cracking morphology and dynamic fracturing mechanism of natural brittle sandstone containing layer structure under compression. Constr. Build. Mater. (2024).
Yun, C., Zhanping, S., Zhiwei, X., Tengtian, Y. & Xiaoxu, T. Failure mechanism and infrared radiation characteristic of hard siltstone induced by stratification effect. J. Mt. Sci. (2024).
Zhao, Y. Study on damage-stress loss coupling model of rock and prestressed anchor cable in dry-wet environment. Int. J. Min. Sci. Technol. (2023).
Ju, Y. et al. Quantification of continuous evolution of full-field stress associated with shear deformation of faults using three-dimensional printing and phase-shifting methods. Int. J. Rock Mech. Min. Sci. 126, 104187. https://doi.org/10.1016/j.ijrmms.2019.104187 (2020).
Article MATH Google Scholar
Zhan-ping, S., Yun, C. & Ze-kun, Z. Y. Teng-tian, Tunnelling performance prediction of cantilever boring machine in sedimentary hard-rock tunnel using deep belief network. J. Mt. Sci. (2023).
Rong, G., Yang, J., Cheng, L. & Zhou, C. Laboratory investigation of nonlinear flow characteristics in rough fractures during shear process. J. Hydrol. 541, 1385–1394. https://doi.org/10.1016/j.jhydrol.2016.08.043 (2016).
Article ADS MATH Google Scholar
Koyama, T., Neretnieks, I. & Jing, L. A numerical study on differences in using Navier–Stokes and Reynolds equations for modeling the fluid flow and particle transport in single rock fractures with shear. Int. J. Rock Mech. Min. Sci. 45, 1082–1101. https://doi.org/10.1016/j.ijrmms.2007.11.006 (2008).
Article MATH Google Scholar
Zhang, Z. & Nemcik, J. Fluid flow regimes and nonlinear flow characteristics in deformable rock fractures. J. Hydrol. 477, 139–151. https://doi.org/10.1016/j.jhydrol.2012.11.024 (2013).
Article ADS MATH Google Scholar
Tzelepis, V., Moutsopoulos, K. N., Papaspyros, J. N. E. & Tsihrintzis, V. A. Experimental investigation of flow behavior in smooth and rough artificial fractures. J. Hydrol. 521, 108–118. https://doi.org/10.1016/j.jhydrol.2014.11.054 (2015).
Article ADS MATH Google Scholar
Li, B., Liu, R. & Jiang, Y. Influences of hydraulic gradient, surface roughness, intersecting angle, and scale effect on nonlinear flow behavior at single fracture intersections. J. Hydrol. 538, 440–453. https://doi.org/10.1016/j.jhydrol.2016.04.053 (2016).
Article ADS MATH Google Scholar
Oron, A. P. & Berkowitz, B. Flow in rock fractures: the local cubic law assumption reexamined. Water Resour. Res. 34, 2811–2825. https://doi.org/10.1029/98WR02285 (1998).
Article ADS MATH Google Scholar
Robert, W., Zimmerman, G. S. & Bodvarsson Hydraulic conductivity of rock fractures. Transp. Porous Med. 23 https://doi.org/10.1007/BF00145263 (1996).
Moutsopoulos, K. N. Exact and approximate analytical solutions for unsteady fully developed turbulent flow in porous media and fractures for time dependent boundary conditions. J. Hydrol. 369, 78–89. https://doi.org/10.1016/j.jhydrol.2009.02.025 (2009).
Article ADS MATH Google Scholar
Qian, J., Zhan, H., Chen, Z. & Ye, H. Experimental study of solute transport under non-darcian flow in a single fracture. J. Hydrol. 399, 246–254. https://doi.org/10.1016/j.jhydrol.2011.01.003 (2011).
Article ADS MATH Google Scholar
Cherubini, C., Giasi, C. I. & Pastore, N. Bench scale laboratory tests to analyze non-linear flow in fractured media. Hydrol. Earth Syst. Sci. 16, 2511–2522. https://doi.org/10.5194/hess-16-2511-2012 (2012).
Article ADS MATH Google Scholar
Rong, G., Hou, D., Yang, J., Cheng, L. & Zhou, C. Experimental study of flow characteristics in non-mated rock fractures considering 3D definition of fracture surfaces. Eng. Geol. 220, 152–163. https://doi.org/10.1016/j.enggeo.2017.02.005 (2017).
Article Google Scholar
Chen, Z., Narayan, S. P., Yang, Z. & Rahman, S. S. An experimental investigation of hydraulic behaviour of fractures and joints in granitic rock. Int. J. Rock Mech. Min. Sci. 37, 1061–1071. https://doi.org/10.1016/S1365-1609(00)00039-3 (2000).
Article MATH Google Scholar
Brush, D. J. & Thomson, N. R. Fluid flow in synthetic rough-walled fractures: Navier-Stokes, Stokes, and local cubic law simulations. Water Resour. Res. 39 https://doi.org/10.1029/2002WR001346 (2003).
Gao, M. A new theoretical model for the nonlinear flow in a rough rock fracture under shear. Computers and Geotechnics (2024).
Ranjith, P. G. & Darlington, W. Nonlinear single-phase flow in real rock joints. Water Resour. Res. 43 https://doi.org/10.1029/2006WR005457 (2007).
Wang, C. et al. Effects of gas diffusion from fractures to coal matrix on the evolution of coal strains: Experimental observations. Int. J. Coal Geol. 162, 74–84. https://doi.org/10.1016/j.coal.2016.05.012 (2016).
Article ADS CAS MATH Google Scholar
Liu, R., Li, B., Jiang, Y. & Huang, N. Review: Mathematical expressions for estimating equivalent permeability of rock fracture networks. Hydrogeol. J. 24, 1623–1649. https://doi.org/10.1007/s10040-016-1441-8 (2016).
Article ADS MATH Google Scholar
Yeo, I. W., Freitas, M. H. D. & Zimmerman, R. W. Effect of shear displacement on the aperture and permeability of a rock fracture, (n.d.).
Esaki, T., Du, S., Mitani, Y., Ikusada, K. & Jing, L. Development of a shear-¯ow test Apparatus and Determination of Coupled Properties for a Single rock Joint (International Journal of Rock Mechanics and Mining Sciences, 1999).
Yin, Q. et al. Hydraulic properties of 3D rough-walled fractures during shearing: An experimental study. J. Hydrol. 555, 169–184. https://doi.org/10.1016/j.jhydrol.2017.10.019 (2017).
Article ADS MATH Google Scholar
Tse, R. & Cruden, D. M. Estimating joint roughness coefficients. Int. J. Rock. Mech. Min. Sci. Geomech. Abstracts. 16, 303–307. https://doi.org/10.1016/0148-9062(79)90241-9 (1979).
Article Google Scholar
Zhao, J. Joint surface matching and shear strength part B: JRC-JMC shear strength criterion. Int. J. Rock Mech. Min. Sci. 34, 179–185. https://doi.org/10.1016/S0148-9062(96)00063-0 (1997).
Article MATH Google Scholar
Park, J. W. & Song, J. J. Numerical method for the determination of contact areas of a rock joint under normal and shear loads. Int. J. Rock Mech. Min. Sci. 58, 8–22. https://doi.org/10.1016/j.ijrmms.2012.10.001 (2013).
Article MATH Google Scholar
Liu, X., Zhu, W., Yu, Q., Chen, S. & Guan, K. Estimating the joint roughness coefficient of rock joints from translational overlapping statistical parameters. Rock. Mech. Rock. Eng. 52, 753–769. https://doi.org/10.1007/s00603-018-1643-6 (2019).
Article ADS MATH Google Scholar
Xiong, X., Li, B., Jiang, Y., Koyama, T. & Zhang, C. Experimental and numerical study of the geometrical and hydraulic characteristics of a single rock fracture during shear. Int. J. Rock Mech. Min. Sci. 48, 1292–1302. https://doi.org/10.1016/j.ijrmms.2011.09.009 (2011).
Article MATH Google Scholar
Xie, L. Z., Gao, C., Ren, L. & Li, C. B. Numerical investigation of geometrical and hydraulic properties in a single rock fracture during shear displacement with the Navier–Stokes equations. Environ. Earth Sci. 73, 7061–7074. https://doi.org/10.1007/s12665-015-4256-3 (2015).
Article ADS MATH Google Scholar
Bordier, C. & Zimmer, D. Drainage equations and non-darcian modelling in coarse porous media or geosynthetic materials. J. Hydrol. 228, 174–187. https://doi.org/10.1016/S0022-1694(00)00151-7 (2000).
Article ADS MATH Google Scholar
Zeng, Z. & Grigg, R. A criterion for non-darcy flow in porous media. Transp. Porous Med. 63, 57–69. https://doi.org/10.1007/s11242-005-2720-3 (2006).
Article CAS MATH Google Scholar
Wang, C. et al. Experimental study of the nonlinear flow characteristics of fluid in 3D rough-walled fractures during shear process. Rock. Mech. Rock. Eng. 53, 2581–2604. https://doi.org/10.1007/s00603-020-02068-5 (2020).
Article ADS MATH Google Scholar
Schrauf, T. W. & Evans, D. D. Laboratory studies of gas flow through a single natural fracture. Water Resour. Res. 22, 1038–1050. https://doi.org/10.1029/WR022i007p01038 (1986).
Article ADS MATH Google Scholar
Download references
This research was supported by National Natural Science Foundation of China (No. 52264006, No. 52064006, and No. 52164001), the Guizhou Provincial Science and Technology Foundation (No. GCC[2022]005 − 1), Specialized Research Funds of Guizhou University (Grant No. 201903, No. 202011).
College of Civil Engineering, Guizhou University, Huaxi District, Guiyang, 550025, Guizhou, China
Tao Wei, Chaolin Wang, Yu Zhao, Mingxuan Shen & Zhongqian Chen
You can also search for this author in PubMed Google Scholar
You can also search for this author in PubMed Google Scholar
You can also search for this author in PubMed Google Scholar
You can also search for this author in PubMed Google Scholar
You can also search for this author in PubMed Google Scholar
“Tao Wei, Chaolin Wang, Yu Zhao, Mingxuan Shen, and Zhongqian Chen wrote the main manuscript text and Zhongqian Chen prepared Figs. 1-4. All authors reviewed the manuscript.”
Correspondence to Yu Zhao.
The authors declare no competing interests.
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
Reprints and permissions
Wei, T., Wang, C., Zhao, Y. et al. Numerical study on the evolution characteristics of contact and fluid flow in shear-induced rough joint. Sci Rep 14, 30971 (2024). https://doi.org/10.1038/s41598-024-82008-3
Download citation
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-024-82008-3
Anyone you share the following link with will be able to read this content:
Sorry, a shareable link is not currently available for this article.
Provided by the Springer Nature SharedIt content-sharing initiative
Advertisement
© 2024 Springer Nature Limited
Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.
