Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.
Advertisement
Scientific Reports volume 14, Article number: 30689 (2024)
Metrics details
In this study, we employed a modeling approach to describe how changes in age-specific epidemiological characteristics, such as behaviour, i.e. contact patterns, susceptibility and infectivity, influence the basic reproduction number (R_0), while accounting for heterogeneity in transmission. We computed sensitivity measures related to (R_0), that describe the relative contribution of each age group towards overall transmission. Additionally, we proposed a new indicator that provides the expected relative change in the number of new infections, given a public health intervention. Studying the outbreak of COVID-19 in Portugal during March 2020, our results show that the main drivers of transmission were individuals 30–59 years old. Furthermore, by studying the impact of imposed changes in susceptibility and infectivity, our results demonstrate that a 10% decrease in susceptibility for the 30–39 years old results in a incidence reduction after 3 generations of approximately 17% in this age group and 4–6% reduction as an indirect effect in the remaining age groups. The presented methodology provides tools to inform the allocation strategy of mitigation measures in an outbreak of an infectious disease. Its inherent versatility enables the easy incorporation of data specific to various populations, facilitating a comparative analysis of epidemic control effects across different countries.
At the early stage of a pandemic, it is crucial to comprehend the global transmission potential of the virus in the population, quantifiable by, e.g., the basic reproduction number, denoted as (R_0). This number delineates the per-generation count of infections caused by a typical infected individual in a fully susceptible population. The reproduction number is influenced by epidemiological characteristics, such as susceptibility and infectivity to the virus in the population. Susceptibility pertains to the set of individual characteristics that allow for infection, such as lower immunity, and may be tied to age. Infectivity, on the other hand, refers to both the virus and individual traits that facilitate transmission, including a higher viral load. Notably, in the case of SARS-CoV-2, both susceptibility and infectivity at the onset of the pandemic were positively correlated with age1,2. Consequently, understanding the impact of age-dependent susceptibility and infectivity is paramount for developing tailored public health interventions.
The extensive use of mathematical modeling and statistical analysis in the study of COVID-19 data has played a significant role in guiding public health policymakers during critical phases of the pandemic. These methods have been employed in an effort to tackle the challenge of quantifying and understanding the impact of non-pharmaceutical interventions, such as lockdowns, school closures, and guiding the strategic allocation of COVID-19 vaccines3,4. Among these methods, the Next Generation Approach (NGA) stands out as a tool for inferring relevant epidemiological parameters in a simple and straightforward manner, especially when compared to traditional compartmental models. Importantly, the NGA maintains an intuitive epidemiological interpretation, making it advantageous in the pandemic context, where the estimation of these parameters can rapidly and effectively inform public policies5,6,7. This approach has proven valuable in previous applications, such as obtaining optimal strategies for vaccine allocation in the Netherlands8,9, studying the evolution of age-specific parameters and an analysis of the reproduction during the early phases of COVID-19 epidemic in Belgium5,6.
The next-generation approach employs the use of the so-called next generation matrix (NGM or (textbf{K})), which directly derives from traditional compartmental models (e.g., SIR model). In a population divided into epidemiologically relevant groups, such as age groups, each matrix entry (represented by (k_{ij})) corresponds to the average number of new infections in group i potentially generated by one individual in group j after one generation. The largest eigenvalue of (textbf{K}) corresponds to the basic reproduction number (R_0). The sum of all the elements in a column represents the average number of infections that one infected individual in group j could potentially generate per-generation in the population, i.e., the group-specific transmission potential ((mathbf {k_{cdot j}})). In the context of the NGA, the mean generation time includes the period during which an individual can infect, thus creating ’offspring’ that will subsequently infect during their generation. This concept creates a parallelism with demographics. In this study we formulate the NGM as the product of a social contact matrix10,11, with diagonal matrices related to the susceptibility and infectivity profile of the population.
This approach also facilitates the estimation of sensitivity indicators5, which quantify how changes in epidemiological parameters would affect (R_0) and relative incidence of the disease-i.e., the distribution of infections across heterogeneous classes. It enables us to estimate the effects of changes in the characteristics of a single group, on the reproduction number. These changes can occur by means of a public health intervention, which can encompass alterations in their infectivity and susceptibility profiles. The resulting changes in the (R_0) and relative incidence are expressed in terms of elasticity values5,12, quantifying the proportional impact of the targeted intervention.
In Portugal, the first COVID-19 cases were reported on March 2, 2020. The number of cases continued to rise until an eventual decline associated with the closure of schools followed by a nationwide lockdown. This decline occurred in early April 2020, marked by a sharp reduction in COVID-19 cases. While several modeling studies have investigated the impact of the first lockdown in March 20203,4,13 and the rollout of the vaccine3,13 in Portugal, to our knowledge, no study has systematically evaluated the importance of each age group and their associated susceptibility and infectivity profiles in disease transmission and age-specific relative incidence. In this study, we apply the next-generation approach to analyze the early outbreak of COVID-19 in March 2020 in Portugal. Our focus is on understanding the contribution of each age group and their associated susceptibility and infectivity profiles to disease transmission. Additionally, we propose a novel indicator within this methodology termed Relative Impact (RI), which gives a relative measure of the impact of an intervention on the number of infected individuals, compared with no intervention in the reference scenario. This method, along with the new indicator, could be particularly valuable in providing prompt responses during a pandemic. Specifically, we calculate sensitivity indicators for the basic reproduction number to measure the relative contribution of each age group towards (R_0). Moreover, we employ the RI indicator to simulate possible interventions, evaluating the impact of a reduction in susceptibility and infectivity for different age groups. In the methods section, we describe the main sensitivity indicators associated with (R_0) and RI, along with their epidemiological interpretation. The mathematical formulation is presented in the supplementary material.
This study, focusing on the early outbreak of COVID-19 in Portugal (01-03-2020 to 30-03-2020), aims to demonstrate how the Next Generation Approach can efficiently inform the dynamics of disease spread by summarizing data into interpretable epidemiological indicators in a fast and straightforward manner. This is particularly crucial in a pandemic context. The results obtained have the potential to inform public health policy during outbreaks of diseases with similar characteristics or can be adapted for different epidemic settings.
The transmission process is described through the next generation operator14 which, by means of linearization around the disease-free equilibrium, allows us to approximate the process of new infections in a matrix form. An explicit formulation of the next generation operator can be derived for any compartmental model7. In the setting of a susceptible-infectious-removed model with a discrete age structure, this process is given by a (ntimes n) matrix (textbf{K}), where n corresponds to the number of age classes. (textbf{K}) is referred to as the next generation matrix, in which (k_{ij}) corresponds to the average number of infections created by an individual in age group j, in age group i throughout the course of its infection, (i,j=1,…,n)7. Matrix (textbf{K}) can be expressed as
where A and H are diagonal matrices with entries related to the susceptibility and infectivity for each age group, respectively. Entry ([A]_{ii}) corresponds to the per contact probability of infection, of an individual in group i, given an infectious contact and ([H]_{ii}) gives the per contact probability of an individual in group i infecting a susceptible individual. These quantities arise from the social contact hypothesis15 and can be obtained up to a proportionality constant q, usually referred to as q-susceptibility and q-infectivity, respectively6. The parameter q accounts for the infectious period and other aspects that might affect the resulting transmission, such as environmental (e.g. seasonality) or social/behavioural (e.g. risk perception) and is calibrated without loss of generality. Matrix (M^{intercal }) corresponds to the contact structure, see the supplementary material for more details.
Matrix (textbf{K}) is used to relate the total number of infections in two consecutive generations11:
where (I_t) denotes the vector of infected by age group in generation t. The entries of (textbf{K}) are positive, yielding a dominant eigenvalue (lambda _1>0) , which can be interpreted as the basic reproduction number (R_0)14,16. Moreover, (textbf{K}) has positive (all entries (>0)) right ((textbf{w}_1)) and left ((textbf{v}_1)) eigenvectors associated with (lambda _1). Eigenvectors can be interpreted up to a non-zero constant. We scale (textbf{w}_1) and (textbf{v}_1) such that (||textbf{w}_1||_1=1) and (langle textbf{w}_1,textbf{v}_1rangle =1). Thus (textbf{w}_1) can be interpreted as the vector of the relative incidence by age group (see supplementary material).
Changes in the epidemiological setting, e.g., vaccination programs, non-pharmaceutical interventions and depletion of susceptibles, will produce a perturbation in the elements of (textbf{K}) and thus in the basic reproduction number and relative incidence. Quantifying these changes is vital to understand the future potential of epidemic growth and the age-specific incidence.
Sensitivity measures assess the response of (R_0) to a perturbation in a given epidemiological parameter. Cumulative elasticities5 are sensitivity measures that can be interpreted as the relative contribution of a specific age group towards the (R_0)12,17,18, i.e. it can ascertain which age groups are the main drivers of transmission. For age group i, (i=1,…,n), it is computed as
where (w_1^{(i)}) and (v_{1}^{(i)}) denote the ith entry of the right and left eigenvectors, respectively.
Elasticity measures can also be obtained for the entries of the relative incidence vector (textbf{w}_1). In this case, sensitivity measures display how the vector (textbf{w}_1) shifts given a perturbation in (textbf{K}).
We can also arrive at a combined measure by considering changes to both (R_0) and (textbf{w}_1). Given a proportional perturbation (p_x in mathbb {R}) on a epidemiological parameter x,
The ratio (RI_j) can be interpreted as an approximation to the relative number of infections, in age group j, in the mth generation after the implementation of an intervention that affected x by (p_x), compared to no intervention, given that no other perturbation in (textbf{K}) occurred up to the mth generation. We note that RI is a projection of the relative measure of the effect of an assumed intervention, where we take the NGM without any alteration as the counterfactual reference.
In Section 6 of the supplementary material, we demonstrated that the error in our approximation of the index RI is influenced by two factors: the magnitude of the considered perturbation, (p_x), and the number of generations, m. By presenting a numerical example, we illustrate that there is an optimal value for the pair ((p_x, m)) that minimises this error, which resulted in considering (m=3) generations. These results are depicted in Figs. S1, S2 and S3. The supplementary material details the mathematical formulation of RI.
We partitioned the Portuguese population in 8 age groups: 0–9, 10–19, 20–29, 30–39, 40–49, 50–59, 60–69, 70+ years old. Data on the number of SARS-CoV-2 positive cases by age group in Portugal was obtained between the period of 2020-03-01 and 2020-03-30 and was used to estimate the relative incidence during the early exponential phase of the pandemic. These data was shared by the group at the Portuguese Directorate General of Health.
The basic reproduction number was set at 2.53,19,20,21, which refers to the transmission potential observed during the early outbreak period in Portugal. Table 1 summarises the relative incidence and infectivity data as well as the estimated q-susceptibility profile of the population. The estimation method is detailed in the supplementary material. Infectivity values were informed by previous modelling works5,6. Pre-pandemic social contact data for the population residing in Portugal was not available. However, a research article22, leveraging contact patterns from the POLYMOD project23 and health survey data, estimated a synthetic social contact matrix for Portugal using Bayesian techniques. This study resulted in a matrix featuring 16 age groups. This was then condensed to include only the 8 age groups considered above, using dimension reduction methods24.
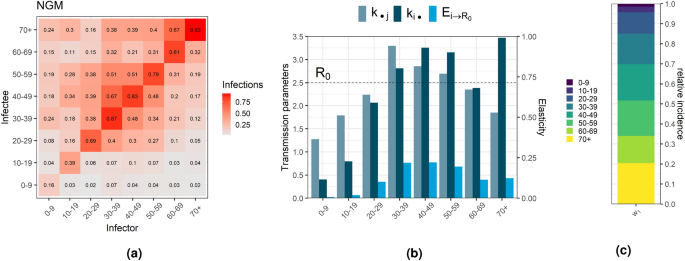
We commence by introducing the next generation matrix, illustrated in Fig. 1a. This matrix was computed using formula (1), detailed in the methods section. We considered that the Portuguese population was partitioned in 8 age groups: 0–9, 10–19, 20–29, 30–39, 40–49, 50–59, 60–69, 70+ years old. Social contact data, infectivity and q-susceptibility data for the Portuguese population was used to inform the NGM. Notably, the age group pair exhibiting the highest transmission is observed among those aged 70 years and above, primarily infecting individuals within the same age group. Following closely are individuals aged 30–39 years, predominantly infecting others within the same age bracket. The pattern observed in the next generation matrix mirrors the outcomes derived from social contact matrices, indicating that assortative contacts22 lead to assortative transmission.
Next generation matrix (textbf{K}) (a). Transmission parameters (R_0), (mathbf {k_{cdot j}}) and (mathbf {k_{i cdot }}) represent the basic reproduction number, average number of infections caused by an individual in age group j in a generation and sum of infections per generation in age group i caused by one individual of each age group, respectively ((j=1,…,8)) (b). Proportion of infections belonging to each age group, (relative incidence vector (textbf{w}_1)) (c).
The relative incidence is illustrated in Fig. 1c. It reveals that, at the onset of the epidemic, the incidence of infections was concentrated in older age groups, with individuals above 50 years old accounting for approximately 50% of the confirmed infections. The column sums of the next generation matrix ((textbf{K})), denoted as (mathbf {k_{cdot j}}) for (j=1, ldots , 8), correspond to the average number of infections produced by an infected individual within a given age group in each generational step. These values are depicted in Fig. 1b, alongside the basic reproduction number. The results indicate that, given infection, individuals aged 30–39 years exhibit the highest transmission potential, followed by those aged 40–49 and 50–59 years. In contrast, the youngest individuals (0–9) demonstrate the lowest transmission potential.
Figure 1b also presents age group estimates for the cumulative elasticity index (E_{irightarrow R_0}). These measure the proportional contribution of each age group towards overall transmission ((R_0)). The results indicate that (R_0) is least elastic to changes in age groups 0–9 and 10–19 years old, and most elastic to changes in age groups 30–39 and 40–49 years old, followed by those 50–59 years old. This suggests that alterations in the behavior or epidemiological characteristics of individuals aged 0–19 years result in the smallest variation in (R_0), while changes in the 30–59 age groups lead to the greatest variations. Specifically, individuals aged 30–39 and 40–49 years contribute equally (22%) to variations in (R_0). However, individuals aged 30–39 years exhibit the highest transmission potential, with an average of 3.3 infections when compared to 40–49 years old, with 2.85. The similar contributions, despite distinct transmission indexes ((mathbf {k_{cdot j}})), result from individuals aged 30–39 being less infected compared to those aged 40–49. This observation is evident when examining the row sums of the matrix (mathbf {k_{icdot }}), (i=1, ldots , 8), which indicate the sum of infections per generation in group i originating from a single infected individual in each age group.
Relative impact (RI) given a 10(%) proportional reduction in q-susceptibility (a) and infectivity (b) for each age group. RI can be interpreted as the projected relative impact of a given intervention (simulated as a reduction to q-susceptibility or infectivity), on the relative number of infected after (m=3) generations, where the counterfactual scenario assumes no intervention.
The relative impact (RI) enables the projection and comparison of the impact of changes in epidemiological parameters on the relative number of infected individuals per generation, where the counterfactual reference is given by the NGM presented in Fig. 1a. We perform these projections to simulate potential interventions related to alterations in the susceptibility and infectivity of each age group. These interventions can include the use of personal protective equipment (PPE), e.g. face masks, which, for COVID-19, have been estimated to reduce transmission by at least 12–18%25. This reduction is achieved through a combination of reduced susceptibility due to mask usage by those who are susceptible and reduced infectivity of those who are infected. Figure 2a displays the RI assuming a 10% reduction in q-susceptibility, for each age group. The results reveal that the greatest decrease in RI is observed when PPE is used by either age groups 30–39, 40–49 or 50–59, aligning with the age groups to which (R_0) is most elastic, see Fig. 1b. As a direct effect of the use of PPE, it is anticipated that, in the absence of other changes, the number of infected individuals after three generations will decrease by approximately 17% and 16% in the age groups 30–39 and 40–49, respectively, when considering no use of PPE as the reference scenario. As an indirect effect, a decrease of approximately 3%-6% is expected in the remaining age groups. Generally, the direct effects of reducing q-susceptibility outweigh the indirect effects for all age groups.
Similar to the results obtained for q-susceptibility, RI is more pronounced when a 10% reduction in infectivity occurs in age groups between 30 and 59 years old, as displayed in Fig. 2b. However, the impact of reducing infectivity is generally smaller than the impact of reducing q-susceptibility, especially as a direct effect on the group where the reduction occurs.
Computing sensitivity and elasticity indicators tied to the next generation matrix provides insights into the underlying dynamics of disease transmission. In a structured population, one can measure the contributions of specific groups to both transmission changes and age-specific relative incidence. Furthermore, it can be used to evaluate the theoretical effectiveness of a given public health intervention.
In this case study, we examined the age group profile of the Portuguese population concerning characteristics related to susceptibility and infectivity to the SARS-CoV-2 virus. Using cumulative elasticities, we demonstrated that the population aged 30–39 and 40–49 years contributes the most to new infections, followed by those aged 50–59 years, with a combined cumulative elasticity value of (64%). These results are in line with similar studies. In particular, in a paper studying the resurgence of COVID-19 cases in mid 2020 in the United States26, the authors estimate that individuals 20–49 years were responsible for 65 out of 100 infections, and those 35–49 years old presented the highest transmission potential. They also concluded a limited role of children in disease spread. Furthermore, a modelling study for the first 2 years of pandemic in the Netherlands27 indicates that seroprevalence among children and adolescents was low, when compared to adults.
Looking at those 40–49 and 70+ years, we observe that although they have similar values for relative incidence, with those 70+ years having a marginally higher value, these occur due to distinct transmission dynamics. Those 40–49 years have a higher amount of contacts and lower susceptibility, while those 70+ have much lower contact rates but higher susceptibility. Resulting in a higher contribution to transmission from those 40–49 when compared to those 70+ years old, as displayed by their elasticity values. An intervention, such as the use of PPE, which reduces q-susceptibility by 10% in those aged 30–39, 40–49 or 50–59 results in a 16%-17% decrease in infections within the same group and a 3%-6% reduction in the remaining groups after three generations. Resulting in the greatest decrease in infections when compared to applying the same intervention in the remaining age groups. The inverse also holds: a proportional increase in q-susceptibility in these groups would lead to a greater increase in new cases compared to the remaining groups. Similar conclusions can be drawn when examining changes in infectivity. These results highlight that these three groups are the main drivers of new infections. Additionally, proportional variations in q-susceptibility and infectivity in the age group 30–39 would result in more significant changes to both (R_0) and RI, compared to the remaining age groups. This result emphasizes how individuals in this age range are the primary drivers of transmission. The previous results also highlight that, while individuals aged 70+ are the most infected, they are not be the most effective target for interventions aimed at reducing transmission.
We highlight that this analysis depends on having data regarding contact patterns of individuals, as well as their q-susceptibility and infectivity profiles. However, such data may not be readily available during the early stages of an outbreak. As an alternative, some authors have proposed using pre-pandemic contact data28,29, mobility data30, or synthetic contact matrices22 to inform contact patterns. Moreover, a limitation of using reported incidence data to inform q-susceptibility, is the fact that individuals with a clinical presentation are more likely to be tested. Consequently, infections in younger age groups, which are more likely to be asymptomatic but still infectious31, may be underrepresented in the testing data32,33. This may result in an underestimation of q-susceptibility and thus may result in an underestimation of their contribution to disease spread. However, our q-susceptibility values are in accordance with literature, where in the early phases of the COVID-19 epidemic, children have been shown to be less susceptible and those above 60 years old are more susceptible to infection2. Moreover, the under ascertainment impact was shown to be limited when looking at the sensitivity analysis5. When available, sero prevalence data can also be used to inform relative incidence, providing an alternative to inform on infection rates.
The approach presented in this study offers a notable advantage by requiring minimal epidemiological data associated with an outbreak to inform transmission patterns. Additionally, it is easily extendable to other diseases, provided that the associated next generation matrix derived has similar properties. Importantly, this approach can be applied cross-sectionally as new data becomes available during an outbreak, allowing for the continuous assessment of the main contributors to disease spread and the projection of the effects of future interventions. In this context, the dominant eigenvalue of the next generation matrix would indicate the effective reproduction number.
Future work entails conducting a similar analysis on the evolution of the reproduction number throughout the COVID-19 pandemic in Portugal and several other European countries. This analysis will assess how different transmission profiles lead to changes in the reproduction number across these countries, facilitating comparisons of epidemics and aiding in the development of country-specific strategies to combat future outbreaks with characteristics similar to COVID-19. Implementing this proposed analysis requires updating the structure of (textbf{K}) to accommodate changes in the epidemiology of COVID-19, including the introduction of new variants and associated characteristics, the spectrum of susceptibility in the population due to previous infection, vaccination and booster doses, waning immunity, as well as changes affecting social contacts.
The datasets analysed during the study are available in the github repository, https://github.com/Liesareus/NGA_paper_data.git.
The methods described were implemented in the Socrates34 online tool. This analysis can be run for the social contact matrices on the website, including the data collected in the CoMiX longitudinal survey28.
Davies, N. G. et al. Age-dependent effects in the transmission and control of COVID-19 epidemics. Nat. Med.[SPACE]https://doi.org/10.1101/2020.03.24.20043018 (2020).
Article PubMed PubMed Central MATH Google Scholar
Goldstein, E., Lipsitch, M. & Cevik, M. On the effect of age on the transmission of SARS-CoV-2 in households, schools, and the community. J. Infect. Dis. 223, 362–369. https://doi.org/10.1093/infdis/jiaa691 (2020).
Article CAS PubMed Central MATH Google Scholar
Caetano, C., Morgado, M. L., Patrício, P., Pereira, J. F. & Nunes, B. Mathematical modelling of the impact of non-pharmacological strategies to control the COVID-19 epidemic in Portugal. Mathematics[SPACE]https://doi.org/10.3390/math9101084 (2021).
Article MATH Google Scholar
Caetano, C. et al. Measuring the impact of COVID-19 vaccination and immunity waning: A modelling study for Portugal. Vaccine 40, 7115–7121. https://doi.org/10.1016/j.vaccine.2022.10.007 (2022).
Article PubMed PubMed Central MATH Google Scholar
Angeli, L. et al. Who acquires infection from whom? A sensitivity analysis of transmission dynamics during the early phase of the COVID-19 pandemic in Belgium. J. Theor. Biol. 581, 111721. https://doi.org/10.1016/j.jtbi.2024.111721 (2024).
Article MathSciNet PubMed MATH Google Scholar
Franco, N. et al. Inferring age-specific differences in susceptibility to and infectiousness upon SARS-CoV-2 infection based on Belgian social contact data. PLoS Comput. Biol. 18, e1009965. https://doi.org/10.1371/journal.pcbi.1009965 (2022).
Article PubMed PubMed Central Google Scholar
Diekmann, O., Heesterbeek, J. A. & Roberts, M. G. The construction of next-generation matrices for compartmental epidemic models. J. R. Soc. Interface 7, 873–885. https://doi.org/10.1098/rsif.2009.0386 (2009).
Article PubMed PubMed Central MATH Google Scholar
Wallinga, J., van Boven, M. & Lipsitch, M. Optimizing infectious disease interventions during an emerging epidemic. Proc. Natl. Acad. Sci. 107, 923–928. https://doi.org/10.1073/pnas.0908491107 (2009).
Article ADS PubMed PubMed Central MATH Google Scholar
Miura, F., Leung, K. Y., Klinkenberg, D., Ainslie, K. E. & Wallinga, J. Optimal vaccine allocation for COVID-19 in The Netherlands: A data-driven prioritization. PLoS Comput. Biol. 17, e1009697. https://doi.org/10.1371/journal.pcbi.1009697 (2021).
Article ADS CAS PubMed PubMed Central Google Scholar
Ganyani, T. et al. Estimating the generation interval for coronavirus disease (COVID-19) based on symptom onset data, March 2020. Eurosurveillance 25, 2000257. https://doi.org/10.2807/1560-7917.es.2020.25.17.2000257 (2020).
Article CAS PubMed PubMed Central MATH Google Scholar
Hurford, A., Cownden, D. & Day, T. Next-generation tools for evolutionary invasion analyses. J. R. Soc. Interface 7, 561–571. https://doi.org/10.1098/rsif.2009.0448 (2009).
Article PubMed PubMed Central Google Scholar
Keyfitz, N. & Caswell, H. Applied Mathematical Demography (Springer, 2010).
MATH Google Scholar
Viana, J. et al. Controlling the pandemic during the SARS-CoV-2 vaccination rollout. Nat. Commun. 12, 3674. https://doi.org/10.1038/s41467-021-23938-8 (2021).
Article ADS CAS PubMed PubMed Central MATH Google Scholar
Diekmann, O., Heesterbeek, J. & Metz, J. On the definition and the computation of the basic reproduction ratio R0 in models for infectious diseases in heterogeneous populations. J. Math. Biol. 28, 365–382. https://doi.org/10.1007/bf00178324 (1990).
Article MathSciNet CAS PubMed MATH Google Scholar
Wallinga, J., Teunis, P. & Kretzschmar, M. Using data on social contacts to estimate age-specific transmission parameters for respiratory-spread infectious agents. Am. J. Epidemiol. 164, 936–944. https://doi.org/10.1093/aje/kwj317 (2006).
Article PubMed MATH Google Scholar
van den Driessche, P. & Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 180, 29–48. https://doi.org/10.1016/s0025-5564(02)00108-6 (2002).
Article MathSciNet PubMed MATH Google Scholar
van den Driessche, P. Reproduction numbers of infectious disease models. Infect. Dis. Modell. 2, 288–303. https://doi.org/10.1016/j.idm.2017.06.002 (2017).
Article MATH Google Scholar
Diekmann, O. & Heesterbeek, J. A. P. Mathematical epidemiology of infectious diseases: Model building, analysis, and interpretation (John Wiley, 2000).
MATH Google Scholar
Davies, N. G. et al. Effects of non-pharmaceutical interventions on COVID-19 cases, deaths, and demand for hospital services in the UK: A modelling study. Lancet Public Health 5, e375–e385. https://doi.org/10.1016/s2468-2667(20)30133-x (2020).
Article PubMed PubMed Central Google Scholar
Prem, K. et al. The effect of control strategies to reduce social mixing on outcomes of the COVID-19 epidemic in Wuhan, China: A modelling study. Lancet Public Health 5, e261–e270. https://doi.org/10.1016/s2468-2667(20)30073-6 (2020).
Article PubMed PubMed Central MATH Google Scholar
Riccardo, F. et al. Epidemiological characteristics of COVID-19 cases and estimates of the reproductive numbers 1 month into the epidemic, Italy, 28 January to 31 March 2020. Eurosurveillance 25, 2000790. https://doi.org/10.2807/1560-7917.es.2020.25.49.2000790 (2020).
Article CAS PubMed PubMed Central Google Scholar
Prem, K., Cook, A. R. & Jit, M. Projecting social contact matrices in 152 countries using contact surveys and demographic data. PLOS Comput. Biol. 13, e1005697. https://doi.org/10.1371/journal.pcbi.1005697 (2017).
Article ADS CAS PubMed PubMed Central Google Scholar
Mossong, J. et al. Social contacts and mixing patterns relevant to the spread of infectious diseases. PLoS Med. 5, e74. https://doi.org/10.1371/journal.pmed.0050074 (2008).
Article PubMed PubMed Central MATH Google Scholar
Hilton, J. & Keeling, M. J. Estimation of country-level basic reproductive ratios for novel coronavirus (SARS-CoV-2/COVID-19) using synthetic contact matrices. PLOS Comput. Biol. 16, e1008031. https://doi.org/10.1371/journal.pcbi.1008031 (2020).
Article ADS CAS PubMed PubMed Central MATH Google Scholar
Boulos, L. et al. Effectiveness of face masks for reducing transmission of SARS-CoV-2: A rapid systematic review. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 381, 20230133. https://doi.org/10.1098/rsta.2023.0133 (2023).
Article ADS MATH Google Scholar
Monod, M. et al. Age groups that sustain resurging COVID-19 epidemics in the united states. Science 371, eabe8372. https://doi.org/10.1126/science.abe8372 (2021).
Article CAS PubMed MATH Google Scholar
Boldea, O., Alipoor, A., Pei, S., Shaman, J. & Rozhnova, G. Age-specific transmission dynamics of SARS-CoV-2 during the first 2 years of the pandemic. PNAS Nexus 3, 24. https://doi.org/10.1093/pnasnexus/pgae024 (2024).
Article Google Scholar
Coletti, P. et al. CoMix: Comparing mixing patterns in the Belgian population during and after lockdown. Sci. Rep. 10, 21885. https://doi.org/10.1038/s41598-020-78540-7 (2020).
Article ADS CAS PubMed PubMed Central MATH Google Scholar
Gimma, A. et al. Changes in social contacts in England during the COVID-19 pandemic between March 2020 and March 2021 as measured by the CoMix survey: A repeated cross-sectional study. PLOS Med.Bold”>19, e1003907. https://doi.org/10.1371/journal.pmed.1003907 (2022).
Article CAS PubMed PubMed Central Google Scholar
Lajot, A. et al. How contact patterns during the COVID-19 pandemic are related to pre-pandemic contact patterns and mobility trends. BMC Infect. Dis. 23, 410. https://doi.org/10.1186/s12879-023-08369-8 (2023).
Article PubMed PubMed Central Google Scholar
Karron, R. A. et al. Assessment of clinical and virological characteristics of SARS-CoV-2 infection among children aged 0 to 4 years and their household members. JAMA Netw. Open 5, e2227348. https://doi.org/10.1001/jamanetworkopen.2022.27348 (2022).
Article PubMed PubMed Central MATH Google Scholar
Guan, W.-J. et al. Clinical characteristics of coronavirus disease 2019 in China. N. Engl. J. Med. 382, 1708–1720. https://doi.org/10.1056/nejmoa2002032 (2020).
Article CAS PubMed MATH Google Scholar
Brodin, P. SARS-CoV-2 infections in children: Understanding diverse outcomes. Immunity 55, 201–209. https://doi.org/10.1016/j.immuni.2022.01.014 (2022).
Article CAS PubMed PubMed Central MATH Google Scholar
Willem, L. et al. SOCRATES: An online tool leveraging a social contact data sharing initiative to assess mitigation strategies for COVID-19. BMC Res. Notes 13, 293. https://doi.org/10.1186/s13104-020-05136-9 (2020).
Article CAS PubMed PubMed Central MATH Google Scholar
Download references
Constantino Caetano acknowledges FCT within the PhD grants “DOCTORATES 4 COVID”, grant number 2020.10172.BD. Luísa Morgado and Pedro Lima also acknowledge FCT within project UIDB/04621/2020 (Center for Computational and Stochastic Mathematics https://doi.org/10.54499/UIDB/04621/2020). Lander Willem gratefully acknowledges support from the Research Foundation Flanders (FWO) (ACCELERATE project G059423N) and the University Research Fund (BOF) from the University of Antwerp. Niel Hens acknowledges funding from the Methusalem-Centre of Excellence consortium VAX-IDEA. This project has received funding from the European Union’s Horizon 2020 research and innovation programme – project EpiPose (Grant agreement number 101003688) and the ESCAPE project (101095619), funded by the European Union. Views and opinions expressed are however those of the author(s) only and do not necessarily reflect those of the European Union or European Health and Digital Executive Agency (HADEA). Neither the European Union nor the granting authority can be held responsible for them.
Departamento de Epidemiologia, Instituto Nacional de Saúde Doutor Ricardo Jorge, 1600-609, Lisbon, Portugal
Constantino Caetano, Irma Varela-Lasheras & Baltazar Nunes
Interuniversity Institute for Biostatistics and Statistical Bioinformatics, Data Science Institute, Hasselt University, Hasselt, Belgium
Leonardo Angeli, Pietro Coletti & Niel Hens
Center for Computational and Stochastic Mathematics, Instituto Superior Técnico, 1049-001, Lisbon, Portugal
Constantino Caetano, Luisa Morgado & Pedro Lima
Department of Mathematics, Instituto Superior Técnico, 1049-001, Lisbon, Portugal
Pedro Lima
Centre for Health Economic Research and Modelling Infectious Diseases, Vaccine and Infectious Disease Institute, University of Antwerp, Antwerp, Belgium
Lander Willem & Niel Hens
Department of Family Medicine and Population Health, University of Antwerp, Antwerp, Belgium
Lander Willem
NOVA National School of Public Health, Public Health Research Center, Comprehensive Health Research Center, CHRC, NOVA University Lisbon, Lisbon, Portugal
Baltazar Nunes
You can also search for this author in PubMed Google Scholar
You can also search for this author in PubMed Google Scholar
You can also search for this author in PubMed Google Scholar
You can also search for this author in PubMed Google Scholar
You can also search for this author in PubMed Google Scholar
You can also search for this author in PubMed Google Scholar
You can also search for this author in PubMed Google Scholar
You can also search for this author in PubMed Google Scholar
You can also search for this author in PubMed Google Scholar
C.C.: Formal analysis, Conceptualization, Methodology, Software, Visualization, Writing- Original draft. L.A.: Conceptualization, Methodology, Writing-Reviewing and Editing. I.V.-L.: Writing-Reviewing and Editing. P.C.: Conceptualization, Methodology, Writing-Reviewing and Editing. L.M.: Conceptualization, Methodology, Supervision, Writing-Reviewing and Editing. P.L.: Methodology, Supervision, Writing-Reviewing and Editing. LW.: Software, Visualization, Writing-Reviewing and Editing. B.N.: Supervision, Writing-Reviewing and Editing. N.H.: Conceptualization, Supervision, Writing-Reviewing and Editing.
Correspondence to Constantino Caetano.
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
Reprints and permissions
Caetano, C., Angeli, L., Varela-Lasheras, I. et al. Identifying the main drivers of transmission in the early phase of the COVID-19 pandemic in Portugal. Sci Rep 14, 30689 (2024). https://doi.org/10.1038/s41598-024-76604-6
Download citation
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-024-76604-6
Anyone you share the following link with will be able to read this content:
Sorry, a shareable link is not currently available for this article.
Provided by the Springer Nature SharedIt content-sharing initiative
Advertisement
© 2024 Springer Nature Limited
Sign up for the Nature Briefing: AI and Robotics newsletter — what matters in AI and robotics research, free to your inbox weekly.
